对数函数的运算法则

对数函数的运算法则

由指数和对数的互相转化关系可得出:

1.两个正数的积的对数，等于同一底数的这两个数的对数的和，即 

2.两个正数商的对数，等于同一底数的被除数的对数减去除数对数的差，即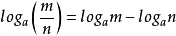

3一个正数幂的对数，等于幂的底数的对数乘以幂的指数，即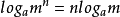

4.若式中幂指数则有以下的正数的算术根的对数运算法则:一个正数的算术根的对数，等于被开方数的对数除以根指数，即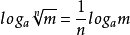

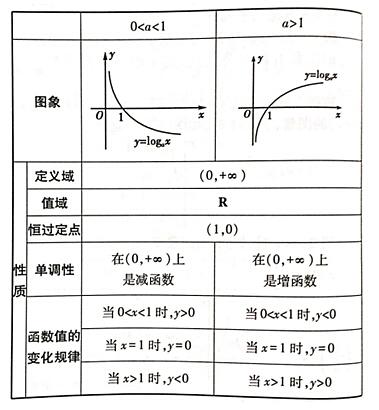
扩展资料：

对数函数y=logax 的定义域是{x 丨x>0}，但如果遇到对数型复合函数的定义域的求解，除了要注意大于0以外，还应注意底数大于0且不等于1，如求函数y=logx（2x-1）的定义域，需同时满足x>0且x≠1和2x-1>0 ，得到x>1/2且x≠1，即其定义域为 {x 丨x>1/2且x≠1}

在实数域中，真数式子没根号那就只要求真数式大于零，如果有根号，要求真数大于零还要保证根号里的式子大于等于零（若为负数，则值为虚数），底数则要大于0且不为1。

在一个普通对数式里 a<0，或=1 的时候是会有相应b的值。但是，根据对数定义：log以a为底a的对数；如果a=1或=0那么log以a为底a的对数就可以等于一切实数。（比如log11也可以等于2，3，4，5，等等）

如果不等于1的正实数，这个定义可以扩展到在一个域中的任何实数  （参见幂）。类似的，对数函数可以定义于任何正实数。对于不等于1的每个正底数 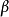 ，有一个对数函数和一个指数函数，它们互为反函数。

参考资料：百度百科——对数运算法则