怎样解三元一次方程组
的有关信息介绍如下:一般三元一次方程都有3个未知数x,y,z和3个方程组,先化简题目,将其中一个未知数消除,先把第1和第2个方程组平衡后相减,就消除了第一个未知数,再化简后变成新的二元一次方程。
然后把第2和第3个方程组平衡后想减,再消除了一个未知数,得出一个新的二元一次方程,之后再用消元法,将2个二元一次方程平衡后想减,就解出其中一个未知数了。
再将得出那个答案代入其中一个二元一次方程中,就得出另一个未知数数值,再将解出的2个未知数代入其中一个三元一次方程中,解出最后一个未知数了。
例子:
①5x-4y+4z=13
②2x+7y-3z=19
③3x+2y-z=18
2*①-5*②:
(10x-8y+8z)-(10x+35y-15z)=26-95
④43y-23z=69
3*②-2*③:
(6x+21y-9z)-(6x+4y-2z)=57-36
⑤17y-7z=21
17*④-43*⑤:
(731y-391z)-(731y-301z)=1173-903
z=-3 这是第一个解
代入⑤中:
17y-7(-3)=21
y=0 这是第二个解
将z=-3和y=0代入①中:
5x-4(0)+4(-3)=13
x=5 这是第三个解
于是x=5,y=0,z=-3

扩展资料:
适合一个三元一次方程的每一对未知数的值,叫做这个三元一次方程的一个解。对于任何一个三元一次方程,令其中两个未知数取任意两个值,都能求出与它对应的另一个未知数的值。因此,任何一个三元一次方程都有无数多个解,由这些解组成的集合,叫做这个三元一次方程的解集。
例如,三元一次方程:
 ,解有无数个。
,解有无数个。
当 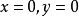 时,
时,  当
当  时,
时, 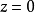
...
当 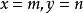 时,
时, 
解三元一次方程组的基本思想仍是消元,其基本方法是代入消元法和加减消元法。
步骤:
①利用代入法或加减法,消去一个未知数,得到一个二元一次方程组;
②解这个二元一次方程组,求得两个未知数的值;
③将这两个未知数的值代入原方程中含有三个未知数的一个方程,求出第三个未知数的值,把这三个未知数的值用一个大括号写在一起就是所求的三元一次方程组的解。
一次方程组,原方程组中的每个方程至少要用一次。
参考资料:百度百科--三元一次方程



