三角函数在生活中的应用

三角函数在生活中的应用

1、比如直角弯管处的接口，如果用两张铁皮制成圆管，并用两棵来垂直相接，那么铁皮的接口处的切线就是它的一部分，只有这样拼接厚才能保证是垂直相接的。

2、三角函数一般用于计算三角形中未知长度的边和未知的角度，在导航、工程学以及物理学方面都有广泛的用途。

3、解决物理中的力学问题时很重要，主要在于力与力之间的转换，并列出平衡方程。

4、利用三角函数，根据地上影子的长度，可以求出大树、旗杆等不便测量的物体的高度。

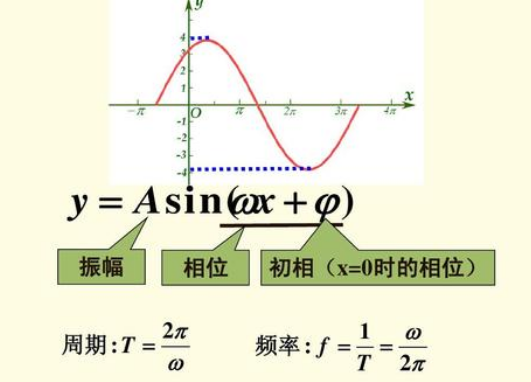
扩展资料

三角函数的起源

公元五世纪到十二世纪，印度数学家对三角学作出了较大的贡献。尽管当时三角学仍然还是天文学的一个计算工具，是一个附属品，但是三角学的内容却由于印度数学家的努力而大大的丰富了。

三角学中”正弦”和”余弦”的概念就是由印度数学家首先引进的，他们还造出了比托勒密更精确的正弦表。

我们已知道，托勒密和希帕克造出的弦表是圆的全弦表，它是把圆弧同弧所夹的弦对应起来的。印度数学家不同，他们把半弦（AC）与全弦所对弧的一半（AD）相对应，即将AC与∠AOC对应，这样，他们造出的就不再是”全弦表”，而是”正弦表”了。

印度人称连结弧（AB）的两端的弦（AB）为”吉瓦（jiba）”，是弓弦的意思；称AB的一半（AC） 为”阿尔哈吉瓦”。后来”吉瓦”这个词译成阿拉伯文时被误解为”弯曲”、”凹处”，阿拉伯语是 ”dschaib”。十二世纪，阿拉伯文被转译成拉丁文，这个字被意译成了”sinus”。

参考资料来源：百度百科-三角函数

参考资料来源：百度百科-正弦三角函数