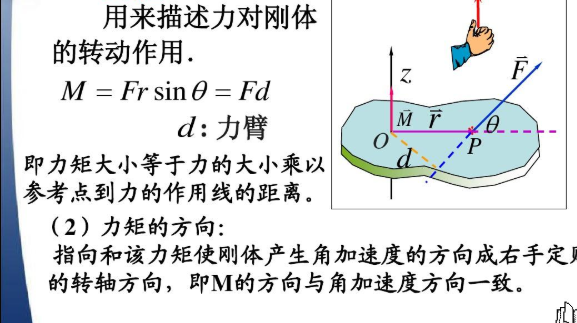
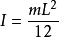力矩的功和转动动能
的有关信息介绍如下:
是刚体运动力学中的东西,去买本普通物理学(程守洙,江之永合编的),哪里都能买第一部分就是 或者http://jpkc.nwpu.edu.cn/jp2005/25/dzjc/p01/ch05/sec05/ 转动惯量知道吧。力矩的功 刚体转动的动能定理力矩的功 如图2-5所示,一个绕固定轴 转动的圆盘状刚体,在圆盘平面上有外力F作用于A点.把力沿法向和切向分解为法向力 和切向力 。圆盘转动时,法向分力 垂直于A点的速度,它不做功.因而外力F的功等于它的切向分力 所做的功,所以:图2—5力矩的功 (2-11)在上式中, 是A点在圆周上的位移元, 是对应的弧长,用 表示与 对应的角位移,有 把上式代入式(2-11),得 上式中的 是外力F对转轴的力矩,于是可以用力矩 表示元功: (2—12) 当刚体从角坐标 转到角坐标 时,外力矩共作功: (2-13) 如果有若干个外力作用于刚体上,先分别计算出每个外力的力矩,求这些外力矩的代数和,得合外力矩.上式中 若是合外力矩,则A就是合外力矩的功. 若 是恒力矩, 与 同方向,力矩做的功相等 二、 刚体的转动动能刚体可以看作是有许多质元所组成的。设各质元的质量分别为m 、 m ….,.各质元与转轴的距离分别为r 、r 、…..,当刚体绕定轴转动时,各质元的角速度ω相等,但线速度各不相同。设其中第i个质元的线速度为 ,其大小为: = r ω, 则相应的动能为: = = = 整个刚体的动能是所有各质元的动能之和, 即 = (2—14 a)将式(2—9a)代入上式中可得: 所以刚体转动动能的表达式为 = (2—14b)三、刚体转动的动能定理力矩对刚体做功是力矩的空间积累过程,将转动定律对角位移 积分得: 上式左边为力矩做的功,右边为 = 即: (2-15) 上式表明:刚体绕定轴转动合外力矩对刚体所做的功时,等于刚体转动动能的增量.这一规律称为刚体转动的动能定理。